TRIGONOMETRY PRACTICE EXAM

Last Updated December 2003

In Problems 1 - 10, use the diagram below to decide whether the given statements are TRUE or FALSE.

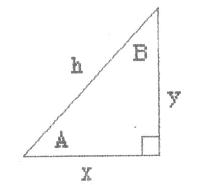
(1)

Ö(x²+y²) = x+y

(2)

  A+B = 90^°

(3)

  sin(A) = sin(B)

(4)

  sin(A) = x/y

(5)

  cos(B) = y/h

(6)

  tan(A) = x/y

(7)

  sec(A) = sec(90^° - A)

(8)

  csc(A) = 1/cos(90^°-A)

(9)

  cos²(A) = sin²(A) - 1

(10)

  tan²(A) = sec²(A) - 1

(11)

If a right triangle has sides of length 2 and 3 meters, what is the length of its hypotenuse?

(12)

What is the exact distance between the points (-1,3) and (2,-3)?

(13)

Use the diagram below to find the measures of the unknown angles and the lengths of the unknown sides.

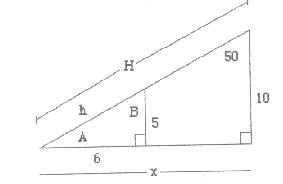
(14)

Find the sum of the angles 60^°55¢15¢¢ and 8^°10¢50^¢¢.

(15)

Convert the angle 35^°30¢15^¢¢ into decimal notation. Round to four decimal places.

(16)

Convert the angle 25.553^° into degree-minute-second notation. Round to the nearest second.

(17)

An angle A in standard position has the point (-1,3) on its terminal side. Fin the exact values of sin(A) and cos(A).

(18)

What are the reference angles associated with A = -210^° and B = 280^°15¢?

(19)

Find the exact value of sec(-210^°).

(20)

A street light rises vertically from a level stretch of ground. A five-foot tall woman standing ten feet from the base of the light casts a twelve-foot shadow. How tall is the street light?

(21)

Convert the angle q = 540^° into radian measure. Do not approximate p.

(22)

Convert q = 31p/18 in degree measure.

(23)

Find the exact value of sin(25p/3). Do not use a calculator.

(24)

The distance from the center of the earth to the moon is about 242,950 miles. If it takes 28 days for the moon to complete one revolution around the earth, approximately how many miles does the moon travel along its orbital path in one week?

Using the triangle shown below, respond to Problems 25-30 by answering TRUE or FALSE.

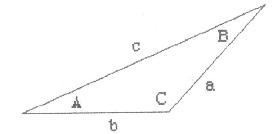
(25)

                     a sinA = b sinB

(26)

                     c sinA = b sinC

(27)

                     b sin(A) = a sin(B)

(28)

                     c² = a²+b² - 2ab cosC

(29)

                     b² = a²+c² - 2ab cosA

(30)

                     a² = b²+c² - 2bc cosA

(31)

One ship spots a lighthouse along the coast on a bearing of N30^° E while another ship, fifteen miles due east of the first, spots the same lighthouse on a bearing of N45^° W. Approximately how far is the lighthouse from each ship?

(32)

Suppose that v is a vector of magnitude 30 and bearing 45^° while w is a vector of magnitude 20 and bearing 150^°. Find the magnitude and the bearing of the resultant v+w.

(33)

A dispute arises over the dimensions of a triangular plot of land. Side a of the property is known to be 150 feet long, and Side b is known to be 50 feet long. Side C lies in a swamp and cannot be measured directly. In court, the defendant claims that he surveyed the property and determined that the angle B between Sides a and C is 30^°. Is the defendant telling the truth?

(34)

In the interval [-p,p] when is sin(x) = 0?

(35)

In the interval [0,2p], when is sec(x) undefined?

(36)

What is the period of the function y = 3+2cos[2(x-p/4)]?

(37)

What is the frequency of the function y = -5+4sin[2(x+p/3)]?

(38)

Find formulas of type y = A+Bsin[C(x±D)] and y = A+Bcos[C(x ± D)] for the graph shown below.

 

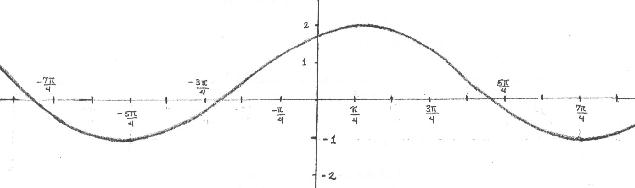
(39)

Find the exact value of Arcsin(sin(-11p/6)).

(40)

Find the exact value of tan(Arcsin(6/7)).

(41)

Using the fact that 255^° = 300^° - 45^°, find the exact value of cos(255^°). Do not use a calculator.

(42)

Find the exact value of cos(2A) if sinA = 3/4.

(43)

Find the exact value of sinA if cos(2A) = -1/4 and A lies in Quadrant III.

(44)

A light pole initially rises vertically from a patch of level ground. After being hit by a strong windstorm, the pole makes an angle of 80^° with the ground. When the sun is 40^° above the horizon, the pole casts a one-hundred foot shadow along the ground. How long is the pole?