There are two important vectors with which we will have to be familiar.  Both of these vectors are related to Newton’s 2nd law:

The summation on the left-hand side of this equation gives us the net, or resultant force acting on the object in question. This net amount of force is  simply given the name The Resultant Force:

If the total force acting on an object equals zero, then the object is said to be in equilibrium.  Often, this is not the case — the sum of the forces, or the  resultant force, does not equal zero. The question then arises: What force would we have to add to the forces acting on the object in order to make the  total force equal to zero? In other words, what force would have to be added in order to leave the object in equilibrium? This force that would have to be added is called the Equilibrant Force:

Now, see if you can following the next lines of reasoning:

We know that equilibrium means that

With the addition of the Equilibrant force, we know that the object is in equilibrium (this is what adding the Equilibrant force means!).  Therefore,  since the sum of all of the forces other than the Equilibrant force is just the Resultant force, we must have that

It then follows that

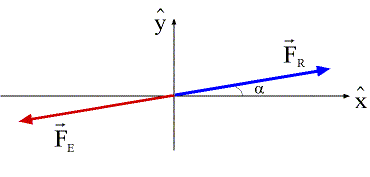
Therefore, if you can find the net or Resultant force, the Equilibrant force is simply the force having the same magnitude, but opposite direction!  For  example, in Ex. 8.3 above, the resultant force is given by

while the Equilibrant force is given by