We now finally get to our first real set of physics equations! Make sure that you understand the meanings of all of the symbols in the equations below, and follow the examples that follow. These equations will take us far in this course, so come to know and love them!

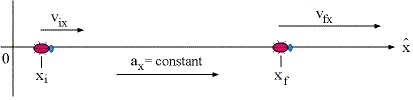
The four 1-D (one-dimensional) kinematic equations of motion are a set of equations which relate the initial and final positions, velocities, acceleration and  time to one another. It will be very important to keep in mind that the following kinematic equations only apply to cases in which the acceleration is a constant!

Consider an object which is at the position x_i at the time t = 0.  At this time it has an x-component of velocity v_ix.  At some time t later, the object is at the  position x_f and is traveling with the velocity v_fx.  During this entire time interval the object is moving with a constant acceleration a_x.  Under these conditions,  the following four 1-D kinematic equations will correctly describe the motion of the object.

# Equation Missing 1 vfx 2 ax 3 xf 4 t

Some notes on solving 1-D kinematics problems are in order before we proceed with the following examples. Click on the “Solving Probs” button at the upper-left to view the notes on Solving 1-D Kinematics Problems.