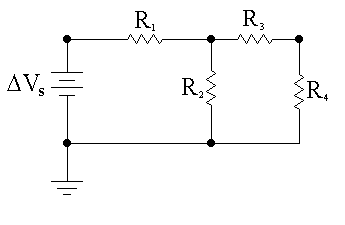
We first reduce the circuit to one involving only the power supply and the equivalent resistance, redrawing the circuit each step of the way. It will be important when you try to solve circuit problems to follow the procedure in applying Method 1 shown  in this and the next two sections as closely as possible.

Figure 14.4

R₃ in series with R₄ (same current: I₃ = I₄ = I₃₄)

By examination of the circuit in Fig. 14.4, it should be clear that the only possible starting point for the combination of resistors is the combination of resistors R₃ and R₄ in series.  (In particular, resistors  R₁ and R₂, or R₁ and R₃ are not in series with one another! Please make sure that this is very clear to you!) By definition of the combination of two resistors in series, we get that

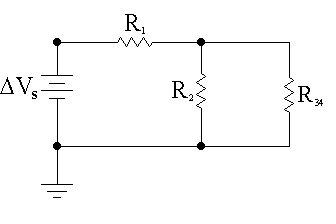
Since we have combined two resistors to find an intermediate equivalent resistance, is important that we redraw the circuit diagram, as shown in Fig. 14.5 below.

Figure 14.5

Note that since R₃ and R₄ were combined in series, the current through the equivalent resistance R₃₄ must be the same as the current flowing through both R₃ and R₄:

R₂ in parallel with R₃₄ (same voltage difference: DV₂ = DV₃₄ = DV₂₃₄)

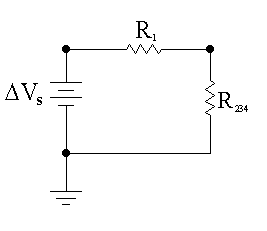
Examination of Fig. 14.5 now shows us that resistors R₂ and R₃₄ are in a parallel combination.  From the definition of a parallel combination of resistors, we get that

Therefore, R₂₃₄ = 1.5 kW.

Figure 14.6

Again, since two resistors have been combined, we redraw the circuit diagram as shown in Fig. 14.6.

Since R₂ and R₃₄ were combined in parallel, they must have the same potential difference across them:

R₁ in series with R₂₃₄:

Finally, an examination of Fig. 14.6 shows us that the resistors R₁ and R₂₃₄ are in a series arrangement. Applying the equation for combining resistors in series, we get that

Note that we’re left with only one resistor, R₁₂₃₄.  This resistor must therefore be the equivalent resistance for the circuit, as given in Eq. (14.7) above. Redrawing the circuit shown in Fig. 14.6 therefore gives us the final circuit shown in Fig. 14.7 below.

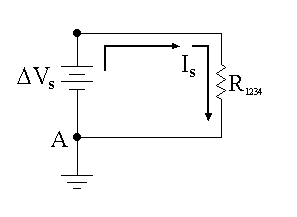Figure 14.7

Since this was a series combination, it follows that the current flowing through resistors R₁ and R₂₃₄ must be the same as the current flowing through the equivalent resistance R₁₂₃₄ = R_e.  This current must be the current supplied by the voltage source, I_s.  We therefore must have that

where we have denoted the current flowing up out of the power source by I_s.