Remember that the magnetic field, and therefore the magnetic flux, through the windings of an inductor (or coil) is often produced by the current through its windings.  It  was found experimentally that the net magnetic flux through an inductor is proportional to the current through its own windings:

To change this proportionality to an equality, we must introduce a constant of proportionality, which in this case we give the symbol L:

The (positive) constant L is called the inductance of the coil, and depends on geometrical factors of the coil (the number of turns, the radius of the coil, its length, etc. Does this sound  reminiscent of our definition of capacitance?  It should!).  The units of inductance must be the units of magnetic flux (tesla meters-squared) divided by current (amps). This combination of units is called one henry(H):

Henry:          1 H = 1 T m²/A.              MKS units of inductance

If the current in the inductor’s windings changes with time, then the magnetic flux will change (since they are proportional). Therefore, since the inductance is a constant for a given inductor,  we get from Eq. (19.3) that

It therefore follows that Faraday’s law can be rewritten in the following special form for inductors:

If the current tries to increase in a certain direction through an inductor, then the induced  potential difference tries to push the excess current back in the other direction in an attempt to keep the current (and therefore the flux) a constant.

The circuit symbol for an inductor is simply a small cylindrical coil of wire:
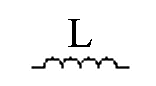