Langston, Cognitive
Psychology, Notes 8 -- Semantic Long Term Memory
I. Goals.
A. Where we are/themes.
B. Traditional (symbolic) models.
C. Neural networks.
II. Where we are/themes. Last time we looked at
episodic memory. This time, we're looking at the way your
knowledge
about the world is organized. As we discussed earlier,
long-term
memory is generally assumed to be divided into autobiographical
memories
(called episodic memory) and fact knowledge (called semantic
memory).
You first learn information in episodic memory, then organize it
into
semantic
knowledge. The topic for this unit is the way that semantic
knowledge
is organized. There are two sides to this problem:
A. What is the structure of the information in semantic
memory?
The first half of this lecture is devoted to "traditional" models,
the
second half to neural networks. Traditional models do a great
job
of explaining the structure. Using carefully controlled
reaction
time studies, they can make and confirm predictions about
organization.
Unfortunately, there are several versions of these models, and they
all
make similar predictions. Neural network models are less
explicit
(in one sense), because they use distributed representations.
B. How does stuff get into semantic memory? What process
sifts through all of your episodes and decides what to abstract as
"facts?"
What process sorts those facts into a higher representation?
These
questions are especially relevant for traditional models, but they
haven't
been answered very well. Neural networks blur the distinction
between
episodic and semantic memories, incorporate learning of information,
and
make these questions less important.
So, the outline will be to look at traditional (symbolic) models and
try to address the two questions. Then we'll look at neural
networks
and do the same thing.
Top
III. Traditional (symbolic) models. A symbol is
something that stands for something else. For example, "MOON"
is
a symbol for the thing in the sky that revolves around the Earth
(really,
any word is a symbol). You're so accustomed to seeing "moon"
used
to refer to the moon that it's hard to separate the two, but there's
nothing
special about the word. It's a relatively arbitrary
arrangement
of
letters that stands for the thing in the sky. It's easier to
see
this in a foreign language. You know what "dog" stands for, so
it
might look like it's the "right" word, but "caine" probably seems
more
arbitrary.
A symbolic model of a cognitive process assumes that you have
symbols
in your head. They are discrete things (easily separable from
one
another) that stand for things in the world. Cognition is
merely
manipulating symbols, a lot like using language is manipulating
symbols.
You arrange words in language to get a meaning ("the dog bit the
man"
means
something different from "the man bit the dog"). You also
arrange
symbols in your head to get a meaning. Our first set of models
will
be symbolic.
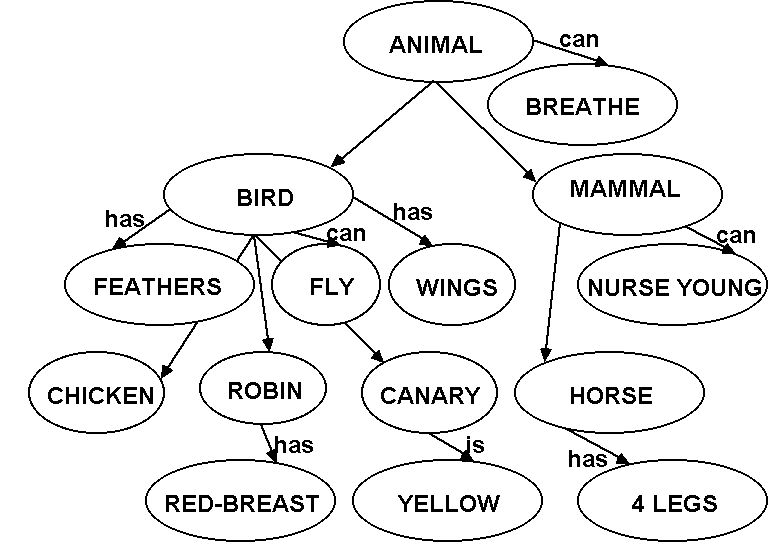
A. Network models. (Collins and Quillian, 1970)
1. Structure. Your concepts are organized in a
collection
of nodes and links between the nodes.
Nodes: Hold the concepts. For example, you have a RED
node,
a FIRE TRUCK node, a FIRE node, etc..
Links: Connect the concepts. Links can be:
a. Superset/subset: ROBIN is a subset of BIRD, so these
nodes are linked.
b. Properties. Nodes for properties are connected to
concept
nodes via labeled property links. For example, WINGS would be
connected
to BIRD via a "has" link.
The nodes are organized in a hierarchy. Distance
matters:
The farther apart two concepts are, the less related they are.
You
also have the concept of cognitive economy: Store things one
time
at the highest place they apply. So, BREATHES is a property of
all
animals, store it at the ANIMAL node instead of with every animal in
the
network. The model included this because it was based on a
computer
model, and computers don't have a lot of memory to spare. It's
not
clear if your brain has the same space limitations. So, this
might
not be an important property of the model. A simple network is
presented
below:
2. Evidence: Do the semantic verification task:
Verify
"a canary is a canary" vs. "a canary is a bird". The more
links
you
have to travel, the longer it takes to verify. Examples:
| Category membership |
Properties |
A canary is a canary.
A canary is a bird.
A canary is an animal. |
A canary is yellow.
A canary has wings.
A canary can breathe. |
As you go down each list of questions, you add more links to travel
before you reach the answer. You get a pattern of response
times
that corresponds to this order. The more links you travel, the
longer
it takes.
3. Problems:
a. Hierarchy: "A horse is an animal" is faster than "a
horse is a mammal". That's not right if it's a hierarchy.
b. Answering no: To say no, the concepts must be far
apart
(a bird has 4 legs). But, saying no is sometimes fastest of
all.
Other times, people are really slow to say "no" ("a whale is a
fish").
Why?
c. Typicality: "A robin is a bird" is faster than "A
chicken
is a bird." A robin is a more typical bird than chicken, but
they're
still one link from the bird concept, so there should be no
difference
in time.
CogLab: We can look at
the results of our lexical decision exercise here and think about
how
that might relate to semantic memory.
B. Feature models. (Rips, Shoben, and Smith, 1974)
1. Structure: Concepts are clusters of semantic
features.
Two kinds of features:
a. Distinctive: The defining features. Sort of
core
features (like wings for birds).
b. Characteristic: Typical features, not required ("can
fly" for birds).
A comparison involves a two step process. First, do a quick
match
on all features. If they're really similar or really
different,
respond
"yes" or "no." If the amount of match is in the middle,
compare
only
distinctive features. Then respond. The distinctive
comparison
involves an extra stage, and should take longer. Here's what
the
model looks like schematically:

Some examples of some features:
|
BIRD |
MAMMAL |
| Distinctive |
wings
feathers
... |
nurses-young
warm-blooded
live-birth
... |
| Characteristic |
flies
small |
four-legs |
|
ROBIN |
WHALE |
| Distinctive |
wings
feathers
... |
swims
live-birth
nurses-young
... |
| Characteristic |
red-breast |
large |
Some types of questions:
| Easy "Yes" |
Easy "No" |
Hard "Yes" |
Hard "No" |
| A robin is a bird. |
A robin is a fish. |
A whale is a mammal. |
A whale is a fish. |
2. Evidence: Use the same verification task. We
can
fix:
a. Typicality effect. More typical members of a category
are responded to faster because they only require one comparison
step.
b. Answering "no." We can explain why some "no"
questions
are harder than others. Also why some "no" questions are
fastest
of all.
c. We also solve the hierarchy problems. It's all due to
similarity, not a hierarchy.
3. Problems: Getting the features is hard
(impossible).
The distinctive features are particularly hard to identify.
Think
how many features of BIRD might not be required for something to
still
be a bird.
C. Spreading activation. (Collins and Loftus, 1975)
1. Structure: It's a network model, but the length of
the
links matters. The longer the link, the less related the
concepts
are. When you search, you activate the two nodes involved, and
this
activation spreads until there is an intersection. The farther
you
go, the weaker the activation gets and the slower it travels.
This
can explain a lot of the findings that were hard for the original
networks.
2. Problem: Making your model really powerful reduces
its
ability to predict. It's not as good when you make a model
over-fit
the data.
CogLab: We'll discuss
the
data from the false memory demonstration and think about how
spreading
activation could be responsible for it.
D. Propositional models.
1. Structure: For propositions, the elements are idea
units
(instead of features). To extract meaning, you get the basic
idea
units and then their relationships. Let's do a sentence:
"Pat practiced from noon until dusk."
The propositions are:
(EXIST, PAT)
(PRACTICE, A:PAT, S:NOON, G:DUSK)
So, we have this thing "Pat," and Pat was the agent of the verb
"practice."
The source of the practice was "noon," and the goal was
"dusk."
The
elements of the proposition are in all caps to indicate that they're
concepts
and not the things themselves.
To extract meaning, extract propositions. This can be a pretty
powerful system if you treat meaning as a grammar. The
elements
are
propositions, the rules come from first-order predicate calculus.
2. Evidence: They can solve some very difficult
problems.
To illustrate, I'll use the problem of scope: How broadly do
we
apply
a quantifier in a sentence? Consider:
"Bilk is not available in all areas."
It could be that Bilk is available in some areas, but not all of
them;
or, Bilk isn't available in all areas (it is available
nowhere).
This kind of ambiguity is not syntactic (based on grammar) and it's
not
lexical (based on word meanings). The problem comes from where
you
apply the "not." Let's use the standard approach to a grammar
of
meaning to understand the sentence.
First-order predicate calculus: Rules to combine propositional
representations:
Symbols:
a. ¬: "It is not the case that."
b. <For
all> x:
"For
all x."
(I couldn't find the upside down capital A)
The "meanings" of the sentence:
a. ¬(<For
all>x) (Bilk is available in
x) (Bilk is only available in some places).
vs.
b. (<For
all>x) ¬(Bilk is available in
x) (Bilk isn't available anywhere).
E. Schemas and scripts. (Bartlett, Schank)
1. Structure: A list of all of the stuff you know about
a concept arranged in some format. Scripts are most
studied.
They are your typical action sequences. For example, you might
have
a restaurant script that tells you the sequence of events at a
restaurant.
The exact structure is a matter of some debate.
2. Evidence:
a. For the use of script knowledge: Pompi and Lachman
(1967)
had participants read a story like the following:
Chief Resident Jones adjusted his face mask while anxiously
surveying
a pale figure secured to the long gleaming table before him.
One
swift stroke of his small, sharp instrument and a thin red line
appeared.
Then an eager young assistant carefully extended the opening as
another
aide pushed aside glistening surface fat so that vital parts were
laid
bare. Everyone present stared in horror at the ugly growth too
large
for removal. He now knew it was pointless to continue.
It's about an operation, but notice that the important words
"doctor,"
"nurse," "scalpel," and "operation" were never used. However,
these
words are part of your operation script (your knowledge of what goes
on
during an operation). When people were given a list of words
to
recognize,
they were likely to "remember" words that were part of the script,
but
weren't presented (like "nurse").
A similar thing occurs if people are asked to remember stories where
script-typical events have been left out. People "remember"
the
missing
parts of the story.
b. How is script knowledge stored? Barsalou and Sewell
(1985) compared two versions: Scripts are organized around
central
concepts or they're organized in sequential order. Let's
demonstrate
their experiment.
Demonstration: Half the class follow the instruction
"write
down everything you can think of related to the task of going to the
doctor,
but generate from the most central action to the least central
action."
The other half follow the instruction "write down everything you can
think
of related to the task of going to the doctor, but generate from the
first
action to the last action." Time for 20 seconds, count the
number
of actions. The sequential group should get more.
The results indicate that the organization of scripts is based on
performance
order and not importance.
F. What do these models have in common?
Abstraction. Some process has to go through what you know and
organize it into concepts (like pick out the distinctive features or
attach
properties to a node). The final concepts are a construct made
from
inputs, not the inputs themselves. This hasn't been very well
explained.
Top
IV. Neural networks. So far, we've been pretty
symbolic
in our analysis of mind. We have symbols (representation) and
rules
that manipulate those symbols (process). Neural networks get
rid
of both. At best we have subsymbols (clusters of elements
whose
joint
operation stands for something else). Instead of a node
holding
some
concept (as in Collins and Quillian) we have a network holding the
concept.
In fact, most of the action is the connections between the
nodes.
The basic idea: Model learning using something that looks like
a
brain (but not a lot like a brain). The idea is to hook up a
lot
of simple processors and have learning emerge from their parallel
operation.
To get an idea, look at the real neuron and artificial neuron
below.
The artificial neuron was based on the real neuron. The neuron
collects
inputs, multiplies them by a weight, and sums them up. Then it
decides
whether or not to fire. If the total input is greater than
some
threshold,
it fires. We can hook a bunch of these together to learn a
problem.

A. Perceptrons. A perceptron is a neuron that learns to
classify. Before we go on, let's make a concept to fit the
methodology
(we need two-valued features).
Taste
Seeds
Skin |
Sweet = 1 or Not_sweet = 0
Edible = 1 or Not_Edible = 0
Edible = 1 or Not_Edible = 0 |
Our examples are:
| Fruit |
Banana |
Pear |
Lemon |
Strawberry |
Green Apple |
| Taste |
1 |
1 |
0 |
1 |
0 |
| Seeds |
1 |
0 |
0 |
1 |
0 |
| Skin |
0 |
1 |
0 |
1 |
1 |
For categorizing: Good_Fruit = 1, Not_Good_Fruit = 0
I've trained the perceptron below to classify the concept good_fruit
(anything with edible skin and seeds). This is its processing
of
banana: It inputs (1,1,0) (for sweet, edible_seeds,
not_edible_skin),
and outputs Not_Good_Fruit. How? It takes each input and
multiplies
it by the weight on the link, then adds them up (1 X 0.0 + 1 X 0.25
+ 0
X 0.25 = 0.25). If that sum is bigger than a threshold (0.4 in
this
case), then it outputs a 1, otherwise a 0. Check its
classification
for the other examples (it should get them all correct).

Now, how does the perceptron learn to classify? Let's train it
on sweet_fruit (sweet is the only feature that needs to be
on).
Start
with all weights at 0.0, and input the first example:

It should call this a sweet_fruit, but it doesn't. So, we want
to adjust the weights to make it more likely to respond sweet_fruit
next
time. How? We use something called the delta rule (also
Hebbian
learning after Hebb, the person who invented it). The idea is
to
make it a little more likely to answer correctly the next time it
encounters
the same problem.
| ∆w = |
learning rate
* (overall teacher - overall output)
* node output |
The learning rate is set to be slow enough to get the right answer
without skipping over it (0.25 for us). The overall teacher is
what
the response should have been, the overall output is what the
response
was, and the node output is the output for a single node (equivalent
to
its input). So, for the taste, seeds, and skin features:
∆w = .25 * (1 - 0) * 1 =
0.25
∆w = .25 * (1 - 0) * 1 =
0.25
∆w = .25 * (1 - 0) * 0 = 0.00
And the perceptron after training on this example is (note, I've
already
put the new example in the input part):

(The weights have been adjusted by adding ∆w
to the old weights.) We're ready to try the next
example.
You
should try each of the remaining examples. The net will
classify
them all correctly once the weights reach the values (0.50, 0.25,
0.25).
I suggest that you work with this until you achieve that set of
weights.
You can stop training after you've learned all of the examples, so
we'll
stop. The concept sweet_fruit is now in the connections in the
net
(it's learned the concept).
B. Some issues for where we are now:
1. We're still doing a lot of work to prepare the concept, but
it's more natural. For example, we could argue that perceptual
systems could
deliver the input coded into the 1's and 0's, and all we did is
adjust
the weights, just like a brain does.
2. We didn't have to understand the classification ourselves
for it to learn. The net figured out how to represent the
information.
That's the magic.
3. We still have a teacher, but you could characterize that as
the environment (as in you touch the stove and the environment tells
you
that was a mistake).
C. Example: Past tense of English verbs. A classic
test case because this acquisition process looks like learning a
rule
and
memorizing exceptions. Early on, kids see a lot of irregulars
and
learn them well. Then they're exposed to all of the verbs
using
the
rule "add -ed for past tense" and they do poorly on
irregulars.
Then
they get good again. If a network can do this, it's strong
evidence
that rules aren't necessary. In fact, networks can learn this.
Plunkett and Marchman (1991) used a perceptron to learn English past
tense, but it was a lot more complicated than our perceptron above.
D. Generalize this: Perceptrons don't work on problems
that aren't linearly separable (you can draw a line between all of
the
positive and negative examples). So, you need a more general
network
that can have internal representations that aren't connected to the
environment.
XOR. The classic problem for perceptrons (as in it's not
linearly
separable, so they can't do it) is XOR (exclusive OR). You
make a
truth table like this:
| Input 1 |
Input 2 |
Output |
1
0
0
1 |
0
1
0
1 |
1
1
0
0 |
For categorizing: 1 = TRUE, 0 = FALSE.
Only say true when one or the other, but not both, of the input
features
is on. You're familiar with XOR from ordering in a
restaurant.
It would be odd to say "I'll have both" when offered the choice of
soup
or salad. The perceptron will fail if you set it up for XOR,
a
network
with a hidden layer will be fine. Demonstrate.
E. Back propagation.
Generalize the delta rule to overcome the problem of linear
separability.
What we need is an internal representation. So, we add a
hidden
layer
(a set of nodes between input and output). Here's a picture
of a
more complicated network:

But, with an internal representation we don't know how to assess
blame
when we're learning. If the network makes a mistake, is it the
link
from input to hidden layer or hidden layer to output? Back
propagation
gets you out of this problem. Instead of a step function (a
linear
activation function), use a sigmoid. This is a curve which
allows
you to do calculus. The mathematics allows you to assign blame
at
all levels of the network. This is a bit beyond us here, but
the
interested student could see me for more information.
Top
Cognitive Psychology Notes 8
Will Langston
Back to Langston's Cognitive Psychology
Page